Le 14 mars a été choisi en 1988 comme journée internationale de célébration du nombre π (Pi), grâce à l’initiative d’un physicien américain. Pourquoi ? Car Pi a pour valeur approximative 3,14 et que le 14 mars s’écrit 3-14 aux USA. Le 14 mars était aussi le jour de naissance d’Albert Einstein. Quel est ce nombre spécial ? Il s’avère que le ratio entre la circonférence d’un cercle et son diamètre est constant, quelle que soit la taille du cercle. Et c’est le même ratio quand on rapporte la surface du cercle par le carré de son rayon. Cette constante a évidemment intrigué la race humaine depuis les temps immémoriaux. D’autant que sa valeur est irrationnelle, c’est-à-dire que l’on ne peut pas l’exprimer par un ratio.
Quel casse-tête !
Comment la tradition juive s’est-elle penchée sur le sujet ?
Ce n’est qu’en 1706 que ce ratio intriguant a reçu un nom, la lettre grecque π (Pi), car il servait à calculer le « périmètre », mot tiré du grec dont la première lettre commence par π. Dès l’antiquité, on a cherché à calculer sa valeur, mais on ne se doutait pas que ce nombre était incalculable, parce qu’irrationnel. Il y a 3 000 à 4 000 ans, les Babyloniens utilisaient le ratio 25/8, ce qui donne 3,1250, et les Égyptiens utilisaient (16/9)2 , ce qui équivaut à 3,1605. Vers l’an 250 avant notre ère, le Grec Archimède avait réussi à circonscrire le nombre Pi entre deux ratios dont le supérieur était 22/7 soit 3,1429. Or Pi est légèrement inférieur à 22/7, car sa valeur commence ainsi : 3,14159. Aussi, le ratio de 22/7 d’Archimède s’est imposé pendant longtemps.
Nos ancêtres Juifs ont, eux aussi, été confrontés à cette valeur énigmatique. Or le Talmud est plutôt étonnant, puisqu’une une Mishna semblait se contenter de la valeur approximative 3, quelque 500 ans après Archimède ! !
« Tout ce qui a une circonférence de trois paumes a un diamètre d’une paume(((Talmud, traité Érouvin, page 13b))). » Mais, les Amoraïm, commentateurs de la Mishna, se doutaient que le ratio 3 était trop court, et ont posé la question :
« Est-ce qu’il ne faudrait pas plutôt une paume((( Talmud, traité Érouvin, page 14a))) et demie ? »
En quelque sorte, approximation pour approximation, ne vaut-il pas mieux utiliser un ratio supérieur (3,5) plutôt qu’inférieur (3) ? Les rédacteurs de la Mishna ont toutefois anticipé cette objection :
« Rabbi Judah [le Saint] a tranché : la traverse est valide si elle est suffisamment large, mais elle n’est pas forte(((Talmud, ibid.))). »
En quelque sorte, on savait que la valeur 3 était approximative, mais que 3,5 était bien trop grand. Comme on le sait aujourd’hui, la valeur réelle est d’environ 3,14 donc plus proche de 3 que de 3,50. Et les Amoraïm de poursuivre cependant le débat :
D’où sont déduits ces calculs ? Rabbi Yohanan a répondu : des Écritures, car il est dit : « Puis il fit le bassin en fonte, de façon parfaitement circulaire, avec dix coudées d’un bord à l’autre, et cinq coudées de hauteur ; une ligne de trente coudées en mesurait le tour(((Rois 7 :23))). »
Il s’agissait du bassin à l’usage des prêtres sacrificateurs (Lévites) pour leurs ablutions dans la cour du Temple, au temps du roi Salomon. S’il avait 10 coudées d’un bord à l’autre, cette valeur est le diamètre du bassin. Or, la circonférence était donnée à 30 coudées, donc avec un ratio de 3, ce qui explique la décision de Rabbi Judah. Mais les Amoraïms, toujours insatisfaits, ont poursuivi :
« Mais sûrement, il y avait [l’épaisseur de] son bord ? ». Rav Papa répondit : « de son bord, il est écrit dans l’Écriture [aussi fin que] la fleur d’un lys(((Rois 7 :26))), car il est écrit : elle avait une paume d’épaisseur et son rebord était travaillé en forme de calices de fleurs de lys. Alors ceci devrait ajouter au moins une fraction ? — Quand [la circonférence] a été indiquée [de 30 coudées], c’était la circonférence intérieure(((Talmud, traité Érouvin, page 14a))). »
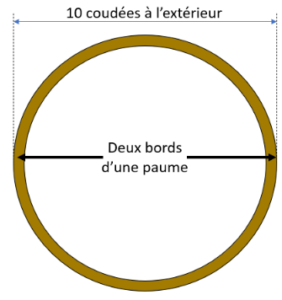
Résumons ce débat : le bassin en fonte ayant 10 coudées de diamètre ‘extérieur’ (car il est dit d’un bord à l’autre), sa circonférence ‘extérieure’ aurait dû être environ 10 x 3,14 = 31,4 coudées. Or le texte biblique nous dit 30 coudées, ainsi le Talmud précise que c’est la circonférence ‘intérieure’. Quelle était l’épaisseur du bord ? Une paume d’épaisseur. La paume avait pour valeur 1/6 de coudée, soit 0,167 coudée. Comme il y a deux bords sur le diamètre extérieur, il faut donc soustraire deux paumes aux 10 coudées, ce qui donne un diamètre intérieur de 9,667 coudées. Or la circonférence intérieure étant de 30 coudées, le ratio cherché est donc ainsi 30 / 9,667 = 3,10 : ceci est une erreur d’approximation de l’ordre de 1 % par rapport à la valeur scientifique de 3,14 (π).
Rabbi Judah n’estimait pas nécessaire d’augmenter de si peu l’approximation de trois, car son but était de donner des règles à l’échelle humaine et non une leçon de calcul abstrait. Et comme l’avait plus tard expliqué Maïmonide, bien en avance sur la preuve de l’irrationalité de Pi au 18ᵉ siècle :
« Il faut savoir que le rapport entre le diamètre du cercle et sa circonférence n’est pas connu et qu’il n’est jamais possible de l’exprimer avec précision. […] Comme on ne le percevra à jamais que comme une approximation, nos Sages ont pris le nombre entier le plus proche […] et ils s’en sont contentés pour leurs besoins de loi religieuse(((Maïmonide, Commentaire de la Mishna (Kitab as-Siraj), section Moèd ))). »
Mais, à y regarder de plus près, le calcul biblique sur le bassin de fonte est donné dans deux textes : I Rois 7 :23 où le mot ‘ligne’ est écrit, comme par erreur, קוה, et dans II Chroniques 4 :2 où le mot ‘ligne’ est correctement écrit קו. On ne peut évidemment supposer qu’un texte sacré soit erroné et il faut plutôt chercher dans de telles ‘erreurs’ un message caché. Or, la guématria de קו est 106, alors que celle de קוה est 111. Si on considère le rapport entre ces deux valeurs, donc 111/106, pour corriger la valeur 3 empirique du texte biblique, on trouve 3 * (111/ 106) soit 3,14151 qui donne le nombre Pi correct cette fois à 4 décimales, avec un écart d’à peine 0,0026 % ! Pour apprécier ce point, il faut rappeler que le Temple de Salomon a été construit vers 1000 avant notre ère, alors qu’une approximation de Pi au-delà de trois décimales n’a été établie en Europe que plus de 2000 ans plus tard.
En résumé, ce n’est pas parce que nos Sages ont utilisé l’approximation de 3 pour établir les lois à l’échelle humaine qu’il faille croire que la connaissance n’était pas à la portée de qui étudiait les textes sacrés. Car comme le Talmud nous prévient :
« La Torah parle avec une phraséologie humaine(((Talmud, traité Baba Metsia, page 31b))). »













